viernes, diciembre 07, 2018

Tiempos imaginarios


La tinta, la crema, el azúcar, o el calor

En la imagen se ve una gota de tinta en agua. Imaginen como se diluye lentamente, volviéndose más transparente. Ese fenómeno se llama difusión.


(CC BY-SA 4.0, by Zvonimir Lončarić)

La difusión es un proceso físico por el que se trasmite energía y materia de un punto a otro del espacio. No sólo a gota de tinta en el agua obedece al fenómeno e difusión
  • Cualquier sustancia (materia) que se pueda disolver en un solvente se difunde en él. La tinta en el agua, el azúcar o la crema en el café, y casi cualquier ejemplo que podamos imaginar.
  • El calor (energía) se difunde en los cuerpos. La resistencia de la plancha genera calor que se difunde en el metal, y al tocar la tela de la camisa también se difunde en ella.
La difusión funciona de un modo muy sencillo, es una tendencia a igualar concentraciones. Se describe con una ecuación bastante simple, que voy a intentar escribir acá. No se asusten, es muy fácil, y es lindo entender cómo se usan las ecuaciones para explicar la realidad.

Supongamos que tenemos una región del espacio con una parte que podemos llamar su interior y una superficie que hace las veces de frontera. Podría tratarse de una gota dentro de un vaso lleno de agua. Supongamos que esa región llena de alguna cosa cuya difusión queremos describir. Por ejemplo, la gota podría contener tinta.


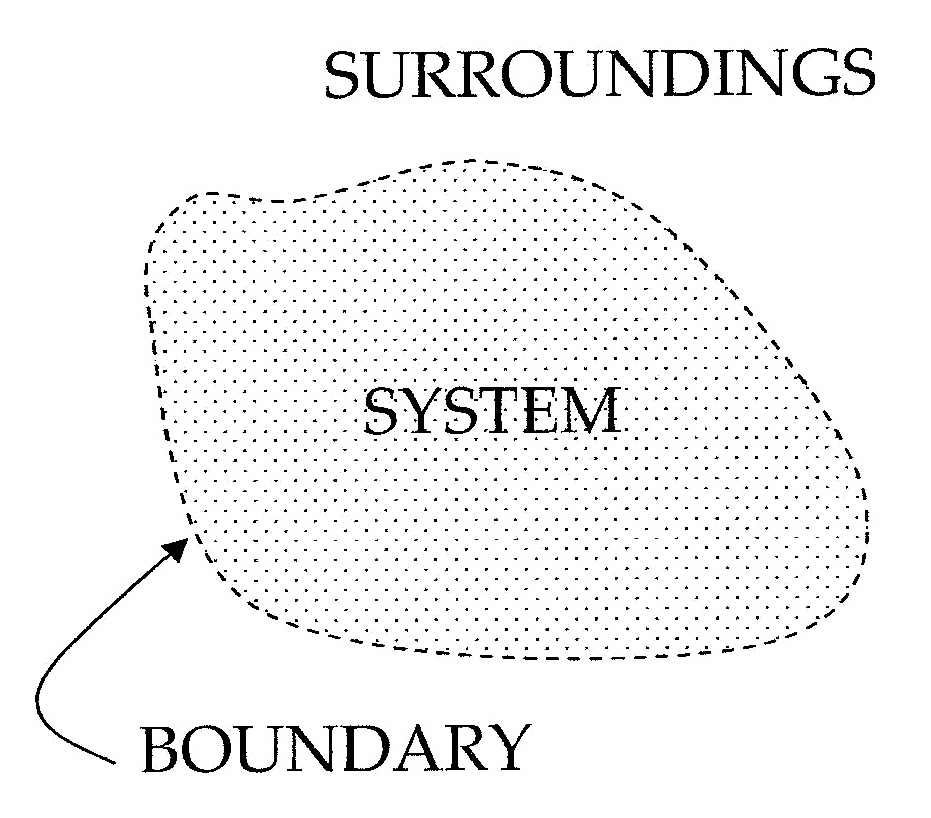
(PD)

El contenido abandonará la región a través de su frontera. La tinta sale de la zona inicialmente más oscura a través de la superficie que rodea esa zona. Podemos establecer una ley sencilla para describir este fenómeno:
La cantidad de contenido que se escapará en cada segundo desde el interior, será proporcional a la diferencia entre la concentración interior y la concentración exterior, y también a la superficie de la frontera.
¿Suena complicado? Leelo de nuevo, es muy sencillo: el mundo tiende a la homogeneidad.
  • Si dentro de la región la tinta está muy concentrada, y fuera está muy diluida, la cantidad de tinta que atraviesa la superficie por segundo será mucha.
  • Si en cambio la concentración dentro es apenas mayor a la concentración fuera, la tinta escapará muy lentamente.
  • Y por supuesto, si la concentración fuera es mayor que la concentración dentro, la tinta entrará en la región en lugar de escapar de ella.
Se trata simplemente de la tendencia a emparejarse que tienen las cosas. Una especie de búsqueda de la homogeneidad.

Escribamos una ecuación para describir el fenómeno. La concentración de tinta es el número de moléculas de tinta dividido el número total de moléculas. O sea, es la probabilidad P de que al tomar una molécula al azar, esta sea de tinta y no de agua.

Si N es el número de moléculas dentro de la región, y dN su cambio en un lapso de tiempo dt, la ecuación es
dN = k (Pe - Pi) S dt
siendo Pe la concentración exterior y Pi la interior, S la superficie de la región, y k una constante que caracteriza el proceso en cuestión.

Esta ecuación de difusión es simplemente la expresión matemática de lo que explicamos antes. Si la fórmula no se entiende, no importa mucho, no contiene nueva información más allá de lo que dice el texto.

Esta ecuación controla los procesos físicos de disolución de materia o de energía. Nos dice como se difunde la tinta en el agua, el azúcar o la crema en el café, o el calor en la plancha.

Los electrones, los protones y demás objetos pequeños


Lo interesante es que la ecuación de difusión se parece mucho a la ecuación de Schrœdinger, que describe la mecánica cuántica de los objetos muy pequeños como las partículas subatómicas.


(PD)

La ecuación de Schœdinger para una partícula se puede escribir así
dN = i h (Pe - Pi) S dt
Donde ahora N es una medida de la probabilidad de encontrar la partícula dentro de la región, Pe y Pi la de encontrarla a cada lado de la superficie, i la raiz cuadrada de -1, y h una constante conocida como constante de Planck.

Como vemos, la ecuación es muy parecida... casi parece que si le cambiáramos el nombre a h y la llamáramos k quedaría igual... salvo por esa maldita i metida ahí adelante... Si quisiéramos leer la ecuación para entenderla en palabras que entendimos la ecuación de difusión ¿Qué rol cumpliría esa i?

La salvedad aquí es que en mecánica cuántica N y P no son realmente probabilidades sino amplitudes, es decir números que en principio pueden ser complejos. Luego podemos identificar nuestra constante de difusión con k = i h, y la interpretación en palabras es la misma que antes
La cantidad de contenido (amplitud) que abandonará la región en cada segundo , es proporcional a la diferencia entre la amplitud interior y la amplitud exterior, y a la superficie de la frontera.
No suena mal. El único problema es que, siendo la amplitud un número complejo, perdemos la intuición acerca de cosas que sem hzan de un lado y de otro de la superficie.

Sin embargo, hay otra interpretación posible. Cambiemos el nombre k = h y redefinamos la manera en la que medimos el tiempo transcurrido como dT = i dt. De nuevo la ecuación se lee así:
La cantidad de contenido (amplitud) que abandonará la región en cada segundo imaginario, es proporcional a la diferencia entre la amplitud interior y la amplitud exterior, y a la superficie de la frontera.
Y o si la amplitud es inicialmente nr el, alo ber una i en la ecuación se mantendrá real al transcurrir el tiempo, y con eso recuperamos la intuición de cosas que se homogeneizan que teníamos con la difusión de la tinta.

Todo muy lindo, pero... ¿qué demonios sería un segundo imaginario?. Y aquí entra el pragmatismo de los físicos: n segundo imaginario es una forma conveniente de transformar la ecuación de Schrœdinger en la ecuación de difusión, manteniendo k real.

Con esta reinterpretación de la ecuación de Schœdinger, podemos decir que los electrones, los protones, o as las partículas subatómicas se difunden en el espacio como si fueran tinta, solo que lo hacen cuando el tiempo corre en la dirección imaginaria.
-- Pero pará, el tiempo el tiempo es un número real, mi reloj no marca números imaginarios. Un tiempo imaginario significa que el universo...
-- ¡Callate y calculá!
Sucede a menudo que situaciones físicas muy diferentes entre sí se vuelven similares si imaginamos que el tiempo pueda ser un número imaginario. Si esto es una simple coincidencia matemática o si tiene alguna interpretación más profunda, es algo que nadie sabe.

Pero ¡guau! ¿no?

Mis posts se publican en
También me pueden contactar en
en

No hay comentarios.:

Publicar un comentario

Nota: sólo los miembros de este blog pueden publicar comentarios.