Nos fuimos a un lugar mejor, sin servicios ni empresas comedatos.

Buscanos en WordPress y en el Fediverso.

Saludos

La breve vida de Boltzmann

La breve vida de Bolzmann

(PD)
Una fluctuación cuántica perturbó la función de onda, enviando un electrón hacia un estado de mayor energía. Esto provocó una deformación en la molécula neurotransmisora, convirtiéndola en el complemento perfecto para el neuroreceptor de la pared de la dentrita. Se unió a él, encajando como piezas de un rompecabezas microscópico.
El estímulo provocó el disparo de la señal neural, compuertas de sodio se abrieron a lo largo del axón, creando una corriente eléctrica que se propagó hacia las neuronas vecinas. Estas reaccionaron a su turno, lanzando también sus chisporroteos, que se difundieron inundando el cerebro. Y en su consciencia, un pensamiento tomó forma:

Esta idea no es real, no es más que una ilusión. Todos mis pensamientos lo son, simples imaginaciones inspiradas en la percepción, que tampoco es real. Mis sentidos no existen, mis ojos, mis oídos, mi piel, no están ahí. Es sólo su fantasma, los efectos de un capricho cuántico en los nervios en mi cerebelo. La mímica convincente de un mundo externo puramente imaginario.
Sólo mi cerebro existe, en un Universo vacío que se expande descontroladamente. Hemisferios, lóbulos, cerebelo y médula espinal. Y tampoco existió siempre, mis recuerdos también son ilusiones. Hace unos instantes sólo había energía en una enorme nada, en una infinita nulidad sin sensaciones. Entonces una fluctuación del vacío me creó de la nada, con toda la historia de mi vida, mis tristezas, mis alegrías, mis imaginarios seres queridos, mis amores, mis odios, mis ilusiones de conocimiento y mis teorías sobre la existencia.
Soy la única mente en el Universo.

El pensamiento inundó su psique, lo llenó de una sensación de comprensión, de plenitud, y de sinsentido.
Y luego todo acabó. En una fracción de segundo la fluctuación del vacío que le había dado origen se disipó. El cerebro se desvaneció, sin ni siquiera un chasquido.
Y el Universo, indiferente, continuó con su expansión desbocada.

Lo que voló con la bomba

(PD)

Este año se cumplieron 74 años de la bomba de Hiroshima. Ese día murieron 250000 personas en una fracción de segundo. Y cambió el mundo. De una forma tan dramática, que se hace difícil verlo hoy, porque cuesta imaginar un contexto diferente.

Junto con el nazismo, las armas nucleares fueron la principal justificación del movimiento anticientífico en la segunda mitad del siglo XX. La izquierda occidental mutó desde su falacia inicial de que marxismo era una teoría científica de la Historia, a su presente desvarío de que la ciencia es un invento capitalista.

Se generaron fábulas sobre cómo la ciencia había justificado al nazismo, cuando en los hechos esas justificaciones nunca tuvieron nada de científicas. Se inventó una visión de la ciencia como la responsable de la bomba atómica, algo que sonaría ridículo si no fuera porque está tan difundido. Peor aún, se creó una doctrina de responsabilidad social de los científicos, como si los logros científicos fueran inventos en lugar de descubrimientos, y entonces el científico pudiera elegir qué descubrir.

(PD)

Se empezó a juzgar a las ideas científicas en términos de su peligrosidad política, como si la realidad tuviera que ajustarse a la medida ideológica humana. En lugar de clarificar que el “racismo científico” nunca fue ciencia, prácticamente se prohibió pensar en el ser humano como un ente biológico. Todavía hoy quien hable de cualquier tipo de diferencia innata entre las personas, será inmediatamente y sin matices tildado de nazi.

Todo eso derivó en un anticientificismo militante, impulsado paradójicamente desde la izquierda y el progresismo en todos los niveles. Y es raro porque hasta la segunda guerra mundial eran los grandes estamentos conservadores los que propugnaban la irracionalidad y el pensamiento mágico en las clases populares. Luego de la Guerra en cambio, el progresismo se puso con entusiasmo la camiseta retrógrada que hasta hacía poco llevaban las iglesias y las oligarquías.

(PD)

El marasmo intelectual en el que el mundo está sumido, desde Trump hasta Macri, tiene mucho que ver con esa actitud de la izquierda de negación y rechazo hacia el conocimiento. En el paupérrimo nivel intelectual del debate público, en Argentina y en el mundo, tal negacionismo progresista tiene una enorme responsabilidad.

Por supuesto que la derecha ayudó, son banales pero no estúpidos. Adoptó el discurso ñoño del progresismo podando cualquier detalle monetario. Con la caída del muro y el fin de los estados comunistas que aún mantenían el positivismo como justificación, el pensamiento posmoderno se hizo dueño de la mente occidental.

Hoy en día el ciudadano de a pié no distingue la ciencia de cualquier cosa que haga un científico. Y lo triste es que buena parte de los académicos, en particular en las áreas humanas, tampoco. Entonces si un científico dice y hace algo deplorable su responsabilidad se traslada del ámbito personal al epistemológico. Fue "a ciencia la responsable del hecho, no la persona del científico.

Por ejemplo, los experimentos secretos con medicamentos en Centroamérica en los 70’s no se discuten como responsabilidad de una decena de políticos y empresarios de EEUU, sino de la ciencia como modo de adquisición de conocimiento. Los 250000 muertos por la bomba de Hiroshima no se achacan a la ambición de poder de Harry Truman sino de la Teoría de la Relatividad y al pobre Albert Einstein.

Se asimila el realismo, la idea de que existe una realidad externa y que podemos entenderla, al autoritarismo de negar opiniones diferentes.

Al no distinguir la ciencia como método, de lo que haga cualquiera que se diga científico, se niega en carácter humano de los científicos. El científico hace ciencia cuando, en un laboratorio, aplica el método al conocimiento de la realidad. No cuando caga o cocina fideos.

(CC0)

Albert Einstein es un lindo ejemplo. Fue pacifista en todas las guerras, algo bastante generalizado en la comunidad científica de entonces y de ahora, que siempre fue muy internacional. De hecho, se opuso abiertamente a ambas guerras mundiales, lo que le valió el desprecio de muchos connacionales.

Su teoría de la Relatividad de 1905 decía que la materia y la energía eran la misma cosa, dos aspectos de la misma cantidad. A alguien se le ocurrió que si se pudiera extraer la energía contenida en un átomo, se podría hacer una bomba. Por supuesto, hecha esa propuesta, los estados imperiales empezaron a investigarla. Pero entre la teoría de la Relatividad y la explosión de Hiroshima pasaron 40 años. En esas décadas se descubrió nada menos que toda la Mecánica Cuántica. No hay absolutamente ningún modo en el que Einstein podría haber previsto en 1905 el resultado de su famoso artículo. Es absurdo siquiera plantearlo.

Ya famoso, Einstein huyó del nazismo y se refugió en EEUU. Allí, firmó una carta de varios académicos dirigida al entonces presidente Franklin D. Roosevelt, alertándolo sobre una posible bomba atómica nazi. Los que atribuyen responsabilidad moral a Einstein por haber firmado esa carta ¿qué hubieran hecho? Era un ser humano, con miedos y dudas. Conocía a Werner Heisenberg que dirigía el programa nuclear alemán, y que no era ningún estúpido. Si los nazis obtenían la bomba, hubieran dominado el mundo. Y aún así dudó, y tuvo que ser convencido por sus colegas para apoyar esa carta.

Son moralmente mucho más ambiguos Julius Oppenheimer o Enrico Fermi, quienes trabajaron directamente en el desarrollo del arma. E incluso así, no tanto: cuando la bomba se ensayó en Alamogordo, New Mexico, varios miembros del Proyecto Manhattan firmaron otra carta, pidiéndole al presidente Harry Truman que no la usara. Sugerían alertar al alto mando japonés de un ensayo en una isla del pacífico, para que pudieran verla, y así forzarlos a la rendición. Pero claro, a esa altura el objetivo de destruir Hiroshima no era detener a los japoneses ni a los nazis, sino asustar a los rusos. La decisión de arrojar la bomba fue una decisión política, y la responsabilidad les cabe a los políticos. No a Einsten ni a la ciencia.

(CC BY-SA 2.0, by romana klee)

Como conclusión: es ya hora de abandonar el negacionismo científico y el relativismo epistémico, porque no debilitan al poder, sino a los sectores populares que deben enfretarlo.

La suerte y las simetrías

(PD)

Un dado cargado es uno que cae preferentemente con una cara particular hacia arriba. En términos matemáticos, la probabilidad de una de sus caras es mayor que la de cualquiera de las otras.

Esto sucede cuando las caras del dado no son equivalentes. En otras palabras, los procesos físicos que tienen lugar cuando lo arrojamos actúan de modo diferente dependiendo de cuál cara esté apuntando hacia arriba en cada instante. De este modo, la dinámica del dado selecciona una cara particular cuando cae al suelo.

El efecto se puede entender razonando en términos de energía: caer con una cara en particular hacia arriba cuesta menos energía que hacerlo con cualquiera de las otras. Si todas las caras costaran la misma energía, entonces no habría preferencia por ninguna de ellas, y todas tendrían la misma probabilidad Habría entonces una simetría entre las caras y el dado no estaría cargado, sería un dado justo… Tal simetría se puede entender intuitivamente si pensamos en tal dado justo apoyado en la mesa sobre una de sus caras: si lo levantamos y lo apoyamos sobre cualquier otra, nada cambia.

Este tipo de situación es general en los sistemas físicos: cuando hay una transformación de simetría (como levantar el dado de la mesa y girarlo) que nos lleva desde un estado cualquiera a cualquier otro, tales estados tienen la misma energía (como las caras de un dado justo) y por lo tanto tienen la misma probabilidad.

(PD)

El fenómeno de diferentes estados que tienen la misma energía se llama degeneración. Cuando hay una simetría aparece una degeneración, y viceversa, cuando encontramos una degeneración inesperada, los físicos saltamos en nuestros laboratorios ¡el sistema nos está ocultando algo! ¡hay alguna simetría escondida allí!

Por ejemplo, estoy estudiando un problema relacionado con los superconductores de alta temperatura crítica, que son una clase de materiales con un interés tecnológico importante. Se pueden dibujar las curvas que representan las energías de los diferentes estados del sistema, como función del campo magnético. Estas curvas se cruzan de a pares en varios puntos, lo que significa que para esos valores del campo magnético la energía de dos estados es la misma. En esos puntos entonces los estados degeneran. En otras palabras, debe aparecer una simetría.

(Imagen propia)

Entender cuál es esa simetría sería muy afortunado, ya que darnos muchísima información sobre los sistemas superconductores… ¡pero no tengo esa suerte!

Heat

Greta Thunberg puso “de moda” el cambio climático, aprovechemos para decir algunas cosas al respecto.

Primero el diagnóstico:

Todas las observaciones indican que hay un incremento en la temperatura global desde la segunda mitad del siglo XX, que se está volviendo virtualmente exponencial en los últimos tiempos. En efecto, los últimos 16 años fueron los más calientes de los últimos 2000, con cada año más cálido que el anterior. Y esa tendencia está acelerándose rápidamente

Absolutamente todas las reconstrucciones de la temperatura pasada dan una media casi un grado menor a la actual, y cuando se extrapolan dan lugar una continuidad del crecimiento de temperatura para los próximos años. La velocidad del calentamiento se duplicó en las décadas transcurridas desde 1950 hasta hoy.

Las zonas más afectadas por el calentamiento son los polos, particularmente en el hemisferio norte. Se registra una reducción del hielo ártico con la consecuente suba del nivel del mar, y un aumento de los fenómenos climáticos violentos debido a los cambios de las corrientes atmosféricas.

El cambio es particularmente rápido en la última década, y se estima que, incluso si ningún parámetro atmosférico se alterara desde hoy en adelante, todavía habría un aumento adicional de al menos medio grado.

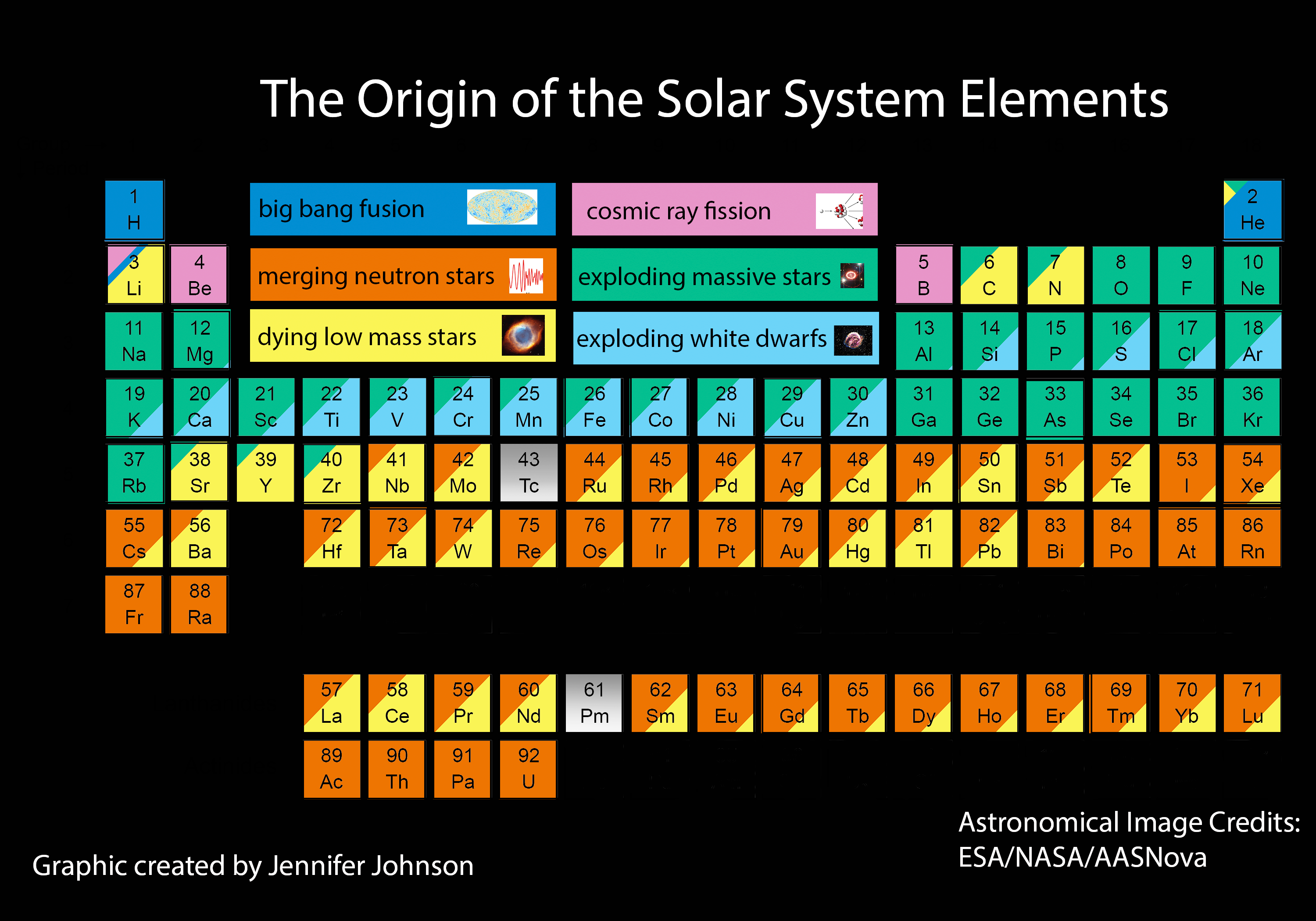
Luego, las causas.

El cambio de temperatura es proporcional a la cantidad de calor acumulada.

Ésta es el resultado del calor que la Tierra recibe, menos el que emite de vuelta al espacio (hay una pequeña cantidad de calor adicional producida en la Tierra, pero podemos considerarla despreciable).

El calor llega a la Tierra en forma de radiación solar. Una parte se absorbe en el suelo y en la atmósfera, y otra se refleja de vuelta al espacio. Una parte de la radiación absorbida se re-emite y también va al espacio. Por eso nuestro punto azul pálido se ve desde tan lejos.

Sin embargo, para que la radiación reflejada pueda llegar al espacio, tiene que dirigirse hacia arriba con la energía suficiente para atravesar la atmósfera en su viaje de salida. Los gases invernadero interceptan a la radiación ascendente, la absorben, y luego la re emiten con menos energía y en cualquier dirección. Por eso, la acumulación de gases invernadero tiene la propiedad de aumentar la temperatura global. El principal gas invernadero es el dióxido de carbono CO2, seguido por el metano NH4 y el vapor de agua H2O.

Otro punto importante es el albedo de la superficie, es decir cuánta de la radiación que recibe la superficie se refleja de vuelta. Las superficies blancas o claras tienen mucho albedo, las negras u oscuras tienen muy poco

Además entran en juego las corrientes marinas, y las atmosféricas, que mueven el calor de un lado a otro en la superficie planetaria, y los vientos, que levantan material particulado (polvillo) en suspensión, lo que a su vez influye en la formación de nubes, las cuales al ser blancas aumentan el albedo.

El sistema climático resultante es muy complejo, y tiene realimentaciones de dos tipos:

• Realimentaciones negativas: es decir cuando las causas producen efectos que mitigan las causas.
  Un ejemplo de realimentación negativa: el calentamiento produce más evaporación del agua de los océanos, que forma más nubes, que así aumentan el albedo y reflejan más radiación, produciendo un enfriamiento.
• Realimentaciones positivas: o sea cuando las causas producen efectos que acentúan las causas
  Un ejemplo de realimentación positiva: el calentamiento derrite el hielo ártico, al desaparecer esa superficie blanca disminuye el albedo, por lo que una cantidad menor de radiación se refleja al espacio, y así se acumula más calor

Luego, los culpables

No hay absolutamente ninguna duda de que el cambio climático es antropogénico, causado por la emisión de CO2 proveniente de los combustibles fósiles. Quien pretenda vender un supuesto “debate científico” al respecto, miente.

La emisión es mayormente industrial, proveniente de quema de combustibles fósiles, principalmente carbón y petróleo, en fábricas y en centrales generadoras de electricidad. El transporte y la calefacción urbanos contribuyen con una parte, que no es despreciable, pero pero no es la parte dominante.

La responsabilidad principal la tienen los países industrializados, particularmente EEUU y China, seguidos por Europa. El lugar de América Latina en las emisiones es muy menor, y la presencia de selvas y bosques en nuestra región contribuye a la recaptación del CO2.

El metano (los flatos de las vacas) no es el principal causante del efecto invernadero. Esa es otra mentira del lobby petrolero para sumar a su causa a su análogo agropecuario, y posponer así la toma de decisiones al respecto. Una segunda contribución, aunque menor, es la emisión de hollín de las chimeneas urbanas e industriales, que oscurece las superficies y disminuye el albedo. Se discute si el hollín, al favorecer la formación de nubes que aumentan el albedo, no tendría en realidad un efecto neutro.

¿Qué va a pasar?

No se sabe muy bien cuánto va a aumentar la temperatura en las próximas décadas, porque los modelos climáticos son muy difíciles de completar. Se estiman entre 1.7ºC y 4.3ºC más en los próximos 100 años incluso si las emisiones de CO2 cesaran completamente hoy mismo. Esto va a tener efectos dramáticos tanto a nivel ecológico como social.

• Aumentarán de fenómenos climáticos extremos (tormentas, inundaciones), la desertificación y los anegamientos permanentes.
  
• Esto afectará preferentemente a los sectores más pobres, que viven en terrenos menos favorecidos. Como consecuencia, habrá migraciones masivas y guerras por territorio.
• La inestabilidad social resultante unida a la autopreservación de la élites privilegiadas, promoverá gobiernos autoritarios, y la necesidad de apropiación de recursos provocará una mayor intervención extranjera en el tercer mundo.
  

Los poderosos del mundo tienen muy claro lo que va a pasar, a pesar de que manifiesten dudas en su discurso público. La extranjerización de la cordillera, por ejemplo, es una muestra de que se están preparando. Lo mismo ese delirio geopolítico de un supuesto “terrorismo dormido” en la triple frontera.

Más allá de los efectos que sabemos tendrá el calentamiento, puede también haber efectos repentinos, debidos a desestabilizaciones no consideradas en los modelos, con consecuencias catastróficas. El descongelamiento del permafrost (hielo subterraneo en Siberia y la Antártida) podría liberar repentinamente una cantidad no conocida de metano enterrado, causando un calentamiento aún más descontrolado. La acidificación y el cambio en concentraciones salinas de los océanos podrían alterar las corrientes marinas causando, paradójicamente, una nueva era glaciar.

Si tenés miedo, es que nos estamos entendiendo.

¿Qué hacer?

Como primer punto, detener la quema de combustibles fósiles. Esto requiere un rediseño de la matriz energética global, algo que no está pasando, básicamente por la incapacidad de las democracias capitalistas para lidiar con los lobbys.

La energía debe provenir de fuentes que no emitan CO2. Si, paneles solares. Sí, energía eólica. Sí, energía geotérmica, y mareomotriz, e hidroeléctrica, y todo eso. Pero no alcanza, necesitamos energía nuclear. Preferentemente fusión, o reactores de fisión de sales fundidas. Eso requiere una inversión en investigación que no se está haciendo. Primero por presión del lobby nuclear, las empresas que fabrican y gestionan reactores de uranio no quieren ser forzadas a un cambio de tecnología. Y aparte por la estupidez del ecologismo moralista, que no sabe nada de pragmatismo.

Pero además, se requiere un re-diseño del orden económico global. El capitalismo industrial necesita del crecimiento económico, para que pueda existir la actividad financiera basada en intereses. Para esto, le resulta crucial el crecimiento poblacional, que es incompatible con la estabilidad climática.

El crecimiento poblacional exponencial, con el consecuente aumento del consumo de recursos y de la deposición de residuos, no es parte de la estrategia de las especies estables, sino que es característico de las plagas.

Y cuando una plaga agota los recursos, se extingue. Y el planeta continúa.

El fuego nos dio el poder para reproducirnos explosivamente y llenar la Tierra. Y ahora el fuego nos está matando. Esta es nuestra prueba, paradójicamente, de fuego: ¿Podremos redefinirnos y salvar este obstáculo? ¿O hemos llegado al final de nuestras capacidades, y sólo nos queda la extinción?

La cientificidad de la astrología

La semana pasada, asistí a un seminario fascinante dictado por mi mentor y modelo de científico Héctor Pipi Vucetich, acerca de la cientificidad de la astrología. Lo que sigue es mi recopilación lo que contó el charlista, agregando tal vez algún detalle de mi cosecha. Las partes aburridas son enteramente mías, el Pipi es incapaz de aburrir.

La pregunta a responder durante la charla fue ¿Es científica la astrología?

(Fuente)

La tentación es responder inmediatamente ¡No! La astrología es una pseudociencia. Pero hacer eso no sería lo correcto: la astrología fue la disciplina fundante de la astronomía, como la alquimia lo fue de la química, o el curanderismo de la medicina. Tenemos hoy algunas disciplinas que llamamos “ciencias” y que aún se hallan en esa etapa inicial. La forma correcta de encarar la cuestión es:

• Primero: preguntarse qué es una ciencia, y establecer lo más formalmente posible su definición. Esto lo podemos hacer siguiendo por ejemplo la epistemología de Mario Bunge.
  
• Segundo: investigar qué es la astrología y cómo la practican sus adeptos. En particular, el Pipi se refirió a los astrólogos “serios” que realizan cartas astrales por encargo siguiendo un método, no a los que inventan los horóscopos de los diarios.
  
• Tercero: ahora sí, responder la pregunta ¿Se adapta la astrología a los criterios de demarcación así establecidos?
  

Recorramos entonces cada uno de esos pasos

¿Qué es una ciencia?

El Pipi resumió la construcción de Bunge, que es extremadamente formal y simbólica, casi como un curso de álgebra, en cuatro puntos fundamentales.

(Fuente)

1. Una ciencia es internamente coherente:
   Una ciencia es un cuerpo de conocimientos, ordenados y organizados en teorías, que son mutuamente coherentes y no contradictorias. La existencia de escuelas mutuamente incompatibles dentro de una dada disciplina pone en duda su cientificidad.
   Por ejemplo, la física es un conjunto enorme de conocimientos, las teorías que la constituyen no se contradicen entre sí. A pesar de la mala divulgación, la mecánica de Newton no contradice a la relatividad en su área común de aplicación: los objetos que se mueven a velocidades muy bajas.
2. Una ciencia presenta coherencia con otras ciencias:
   Las diversas ciencias tratan sobre fenómenos en principio distintos, que a veces resultan ser el mismo fenómeno visto desde diferentes ópticas. En ese caso, no hay contadicciones: las predicciones de las diferentes ciencias son compatibles entre sí.
   Por ejemplo, la biología no contradice a la física, cuando se consideran los seres vivos como sistemas termodinámicos. La segunda ley, que dice que el desorden siempre aumenta, se aplica a sistemas termodinámicos cerrados, mientras que los seres vivos son sistemas abiertos.
3. Una ciencia es contrastable con el experimento:
   Una ciencia hace predicciones acerca de fenómenos observables, que se pueden contrastar con la realidad. Deben ser tales que se pueda distinguir un resultado que las confirme de otro que las contradiga.
   Por ejemplo, la biología, y en particular la evolución darwiniana, predicen que si el ambiente cambia abruptamente, las especies se extinguirán o se adaptarán al nuevo entorno. Si investigamos el registro geológico, comprobaremos que eso es exactamente lo que ha sucedido en el pasado.
4. Una ciencia es revisable de acuerdo a los resultados de la contrastación:
   Finalmente, la ciencia es continuamente revisada y modificada para hacerla compatible con los resultados de las nuevas observaciones. La no revisabilidad y la adhesión a postulados cuyas consecuencias son inconsistentes con las observaciones es un signo de pseudociencia
   Por ejemplo, al notar que el electromagnetismo y la mecánica eran incompatibles a velocidades altas, comenzó una revisión de postulados de la física que terminó en la teoría de la relatividad. La observación de que la radiación de cuerpo negro era incompatible con la mecánica, dio origen a la física cuántica.

¿En qué consiste la astrología?

La astrología se basa en la creencia de que la posición de los planetas en la esfera celeste en un dado momento, influye en la dinámica de los acontecimientos terrestres, incluidos la personalidad y el destino de las personas. Su método consiste en la construcción de cartas basadas en la posición relativa de los cuerpos celestes en un momento determinado. Por ejemplo, una carta natal basada en las posiciones de los planetas en el momento del nacimiento de una persona, permitiría extraer información acerca de su personalidad o de su suerte futuras.

Las cartas se confeccionan de acuerdo a un método bien definido, que se basa en

• Una división de la eclíptica, es decir de la linea imaginaria en el cielo por la que se mueven los planetas, en 12 signos zodiacales diferentes, definidos por las constelaciones que se ven proyectadas detrás. En cada momento del año, los distintos planetas visibles desde la Tierra se encuentran en un dado signo.
  
• A la vez, se divide el cielo visible a una dada hora desde un dado lugar, entre el horizonte al este y el horizonte al oeste, en 12 casas distintas. Al girar la Tierra, las casas giran junto con ella. Por eso a lo largo del día va cambiando qué signo está dentro de cuál casa.
  

Con esto, conociendo con cierta precisión una hora y un lugar, el astrólogo puede reconstruir usando cálculos astronómicos, qué planeta estaba en cuál signo y en qué casa. Las casas, los signos, y los planetas, tienen significados, que el astrólogo usa para redactar su predicción.

Entonces ahora sí, podemos finalmente responder la pregunta:

¿Es científica la astrología?

En otras palabras, los métodos y prácticas antes descriptos ¿cumplen los puntos 1. a 4. enunciados más arriba?

(Fuente)

1. Una ciencia es internamente coherente:
   Si bien los postulados de la astrología son sorprendentemente similares en las tradiciones griega, india y china, hay dentro de ella escuelas que asignan significados diferentes a planetas, signos y casas.
   Esto es una mala señal, aunque de por sí no es determinante. La presencia de escuelas diferentes fue una realidad en varias ciencias modernas en sus etapas iniciales de desarrollo. El punto aquí es que la dirección del avance científico debe ser la de eliminar las diferencias entre ellas. No parece haber sucedido eso eso en el caso de la astrología
2. Una ciencia presenta coherencia con otras ciencias:
   En este punto la astrología falla estruendosamente. Sus postulados se dan de frente con casi cualquier otra ciencia con la que se contrasten.
   Por ejemplo, la astrología es incoherente con la física: ¿de qué modo influyen los planetas sobre la Tierra? De todas las interacciones fundamentales ¿cuál es la que da origen a la influencia plasmada en una carta natal? La gravedad del obstetra es mayor que la de cualquier planeta. También lo es la luz que refleja, y cualquier tipo de radiación electromagnética. ¿O se trata acaso de una interacción nueva aún desconocida? De ser así, entonces ¿como puede dicha influencia propagarse instantáneamente desde la posición de los signos zodiacales hasta la Tierra? ¿se mueve acaso más rápido que la luz?
3. Una ciencia es contrastable con el experimento:
   En esto la astrología cumple la condición fundamental de hacer predicciones contrastables… y en todos los casos en los que fueron testeadas, indistinguibles de una elección al azar. Este punto, si fuera el único, no la haría una pseudociencia, sino sólo una teoría falsa.
   Aquí es donde entra el hermoso experimento hecho por Shawn Carlson, entonces estudiante de física y hoy divulgador y promotor de la ciencia amateur. Carlson se contactó con el National Council for Geocosmic Research, una asociación norteamericana de astrólogos, y acordó con ellos un test de la efectividad de la astrología.
   La asociación propondría 28 de sus miembros. Carlson proveería a cada astrólogo los perfiles psicológicos de tres sujetos, y los datos precisos de nacimiento de uno de ellos. Con esto Los astrólogos determinarían, usando la carta natal, a cuál perfil pertenecían los datos. Si el método astrológico funcionara, el porcentaje de aciertos debería ser mayor al 33% que se obtendría por puro azar…
   …y no lo fue. De hecho fue casi exactamente igual al 33%, lo que demuestra que las cartas natales no predicen mejor que lo que lo haría un dado.
   Otro experimento que demuestra la poca efectividad de la astrología es el de los gemelos horarios. Personas que nacen separadas por menos de cien metros, que es la resolución espacial que tienen las cartas natales, y con pocos minutos de diferencia. Estas personas deberían tener personalidades y destinos similares… y no sucede así, según un estudio hecho con datos de los hospitales londinenses.
4. Una ciencia es revisable de acuerdo a los resultados de la contrastación:
   Aquí la astrología vuelve a fallar. A pesar de los experimentos antes descriptos, los astrólogos no han modificado la teoría para adaptarla a los hechos. Al contrario, siguen estancados en una formulación cuya antigüedad pretenden sea un signo de su certeza.

Conclusión

Con esto terminó Vucetich el análisis de la cientificidad de la astrología.

En conclusión, la astrología no cumple los criterios arriba enumerados para ser una ciencia, y debe ser clasificada como una pseudociencia, junto con la alquimia, la homeopatía, el psicoanálisis, la teoría feminista, y la escuela económica neoliberal.

(Fuente)

Kilonovas

En 2016, el experimento LIGO detectó el paso de ondas gravitacionales provenientes de la fusión de dos agujeros negros. Se trató de un hito científico sin precedentes. Por un lado, por las consecuencias teóricas: se confirman dos predicciones cruciales de la Relatividad General: la propagación de ondas gravitacionales y la existencia de agujeros negros. Por otro lado, por el desafío experimental y tecnológico que implicó realizar dicha observación. Por ese logro, el equipo de LIGO recibió el premio Nobel de física 2017.


(Fuente)

Más adelante, el equipo de LIGO en conjunto con un experimento similar llamado Virgo, detectaron una kilonova es decir el choque y la mezcla de dos estrellas de neutrones. En esa ocasión, dos colaboraciones internacionales (llamadas Fermi e INTEGRAL) detectaron una explosión de rayos gamma proveniente del mismo punto del espacio y coincidente con la fusión. A la vez, seis telescopios de gran escala alrededor del mundo también detectaron la fuente en el espectro visible.
Este logro experimental fue muy importante por varias razones.

Fue la primera observación de un evento de fusión por múltiples canales, y además fue la primera vez que se trató de estrellas de neutrones. Como principal éxito, devela el origen de las explosiones de rayos gamma, eventos cósmicos que venían siendo observados desde hacía décadas, pero cuya naturaleza precisa era desconocida. Esto es de por sí un enorme descubrimiento, como para otro Nobel.


(Fuente)

Pero no se detiene ahí la cosa: la detección de oro en el espectro de la explosión resultante, hecha por el telescopio espacial Hubble, muestra que una parte de los metales pesados que encontramos en el universo se forma en esos eventos.

Sabíamos que, excepto el hidrógeno, el helio y parte del litio, los demás elementos químicos que componen nuestro cuerpo y todo lo que nos rodea se crearon en los hornos nucleares que dan vida a las estrellas. Pero tales hornos son capaces de producir eficientemente sólo los elementos livianos, hasta el hierro, mientras producen muy poca cantidad de elementos más masivos. Algunos elementos pesados se forman en las apoteóticas explosiones de supernova que constituyen la muerte de algunas estrellas. Sin embargo, todavía no constituyen la suficiente cantidad como para explicar la cantidad de oro y plomo que vemos a nuestro alrededor.

Luego de morir, algunas estrellas dejan como resto una estrella de neutrones, que es algo así como un núcleo atómico enorme del tamaño de una ciudad. En ese monstruo, las diferentes partes se mantienen unidas por acción de la gravedad. Si bien es un núcleo demasiado grande como para incluirlo en la tabla periódica, si algún evento violento le arrancara un pedazo, la gravedad en élk sería más débil y el pedazo se disgregaría dando origen a núcleos pesados. Una colisión de estrellas de neutrones como la que se detectó hace precisamente eso. Es decir que LIGO, Virgo y Hubble confirmaron la manera en la que se forman los núcleos pesados. ¡Es para otro Nobel más!


(Fuente)

Y todavía hay tela para cortar. El evento de mezcla detectado ocurrió en otra galaxia. La observación permite medir la distancia a esa galaxia directamente. Las distancias cosmológicas se miden mediante un proceso complejo conocido como escalera de distancias cósmicas. Tal escalera depende de muchos pasos o escalones. Conocemos la distancia a un escalón, con él conocemos la distancia al siguiente, y con él al que va después, y así. Si uno de ellos falla, se arruina todo el proceso. De hecho, eso sucedió en los 80’s con las estrellas conocidas como cefeidas, se descubrió que había un error en la forma en la que se medía su distancia y hubo que recalibrar toda la escalera.

La observación de la kilonova permite saltar varios escalones, midiendo directamente la distancia a una galaxia lejana. Eso es muy importante, porque permitirá confirmar si nuestros modelos de expansión cosmológica son correctos. Es realmente una nueva era para la fisica.


(Fuente)

Esta observación histórica fue hecha por colaboraciones internacionales de cientos de personas, trabajando con equipamientos carísimos. El financiamiento fue completamente estatal y hecho por decenas de países alrededor del mundo. Se trata de un descubrimiento de ciencia básica que redundará en avances técnicos hoy impredecibles dentro de al menos un siglo. Esta es la manera en la que avanza la ciencia, no por entrepreneurs que le venden ideas brillantes a las empresas.

Una nota personal: mi juventud científica transcurrió en una era de ausencia de grandes descubrimientos experimentales, que se nos relataban como cosas del pasado. Eso cambió primero con el satélite WMAP que observó el fondo cósmico de radiación que ahora está siendo explorado con Planck, y espectacularmente en los últimos años con el LHC y el descubrimiento del bosón de Higgs, y con LIGO y las ondas gravitacionales.

Es fascinante, y como científico estoy feliz de que me toque vivirlo.

En la soledad cuántica

Acabo de leer el largamente pospuesto artículo de Max Tegmark sobre la interpretación de muchos mundos de la mecánica cuántica. Interesantísimo.
La mecánica cuántica describe el universo en términos de una función de onda que es un número que toma un cierto valor para cada evento posible, y que nos da la probabilidad del evento. Por ejemplo, al arrojar una moneda la función de onda toma un valor para el resultado cara y otro para el resultado ceca.

CC0
Esta descripción probabilista implica que la mecánica cuántica sólo puede aplicarse a sistemas sobre los cuales podamos medir probabilidades. Esto quiere decir que tenemos que ser capaces de realizar el mismo experimento muchas veces, y contar cuántas veces aparece cada resultado posible. Por ejemplo, para comprobar si la función de onda nos dice lo correcto sobre nuestra moneda, repetimos el experimento reitereadamente y vemos si el número de veces que sale cara o ceca se corresponde con su probabilidad.
Sin embargo, cuando queremos pensar en la mecánica cuántica como una descripción del Universo todo, se plantea un problema: no podemos calcular probabilidades sobre el Universo, porque no podemos repetir la evolución cosmológica reiteradas veces.
Para conciliar la idea de un único universo determinista con los resultados cuánticos probabilistas, se han propuesto varias interpretaciones de la mecánica cuántica, la mayoría de las cuales son variantes de la Interpretación de muchos mundos, originalmente desarrollada por Hugh Everett en su tesis doctoral.
Según esta interpretación, cada vez que ocurre un evento, la historia se divide en tantas líneas diferentes como posibles resultados. Y todas son reales. Tiramos una moneda y se crean dos ramas de la realidad, una donde cae cara y otra donde cae ceca. Ambos hechos suceden, ambas posibilidades se hacen realidad. Sendas copias de nosotros experimentan cada una de esas historias, y perciben un mundo donde la moneda eligió unívocamente.
Cada copia de nuestro yo, desde su perspectiva llamémosla de rana, ve a la moneda realizar una elección al azar entre dos opciones. Sin embargo desde una perspectiva platónica o de pájaro, la moneda nunca optó, sino que ambos mundos se hicieron realidad. A cada uno de nuestros avatares rana sólo le importa lo que ve en la rama de la historia en la que vive. Por eso ve un universo probabilista donde cada evento cuántico se decide al azar con una probabilidad dada por la función de onda.

PD
Si existiera un pájaro capaz de ver toda la escena, vería el mundo abrirse a cada instante en una infinidad de historias posibles, cada una de las cuales tiene una función de onda que evoluciona de un modo completamente determinista.

CC0
La perspectiva de rana no solo explica el azar cuántico, sino que en sí misma redefine nuestra mortalidad. Cada rana percibe la rama de la historia en la cual existe. Aquéllas ramas en las que no hay copias porque la rana murió le resultan irrelevantes. Si un resultado de la moneda nos costara la vida, sólo habría una copia de nosotros en la rama de la historia que tuvo el resultado complementario.
Tegmark propone el suicidio cuántico para ilustrar esta idea: un experimentador se pone delante de una ametralladora que dispara o no de acuerdo al resultado de una medida cuántica. Si la monda cae cara, ¡bang!, si la moneda cae ceca ¡click!. El experimentador se sitúa al un lado de la metralleta, y la activa. Naturalmente escuchará ¡bang! ¡bang! ¡click! ¡bang! ¡click! ¡click! ¡bang! ¡click! ¡bang! y así, una sucesión de ¡click! y ¡bang! más o menos al azar. Pero si en cambio se sitúa enfrente de la ametralladora, sólo experimentará aquéllas ramas de la historia en la que siga vivo. O sea que desde su perspectiva, se escuchará ¡click! ¡click! ¡click! ¡click! ¡click! ¡click! ¡click! ¡click! ¡click!
¿Algún voluntario?

PD
Si bien Tegmark es muy cauto, algunos especularon con llevar esta idea un poco más allá. Antes de seguir, dejemos en claro que las interpretaciones de la mecánica cuántica son filosofía, no ciencia. Por lo tanto todo lo que sigue es pura especulación, y no constituye un resultado científico de ninguna clase.
En cualquier evento en el que se jueguen nuestras vidas, por peligroso que fuere, siempre existe alguna posibilidad de sobrevivir. En otras palabras, siempre habrá ramas de la historia en las que sigamos vivos. Como el experimentador con su metralleta, desde nuestra perspectiva subjetiva esas serán las únicas ramas que percibiremos. Siempre esquivamos ese camión, siempre nos curamos del cáncer, y siempre tenemos algo que comer. Nuestro yo subjetivo nos ve inmortales.

CC0
Sin embargo, la restricción de limitarnos sólo a las ramas en las que sobrevivimos no se aplica a las demás personas. Por lo tanto cada uno de nosotros, en la enorme mayoría de las ramas de la historia que podríamos experimentar, se percibirá a si mismo como un inmortal en un mundo de mortales. No pretendo fundar una religión, pero supongo que sobre este planteo se podría incluso escribir un código moral. Aunque creo también que se puede ver como la más deprimente de las perspectivas: tiempo para leer todos los libros, subir todas las montañas, pelear todas las guerras, y cruzar todos los mares… y nadie a quien contárselo.

Cómo ubicar giles usando un GPS

¿Sabés cómo funciona el GPS? Es muy interesante.

(Fuente)

El sistema está formado por una red global de satélites, cada uno de los cuales se comunica independientemente con los dispositivos terrestres, tales como nuestros teléfonos celulares o el equipo de navegación de nuestro auto.

Cada satélite emite una señal de radio que se aleja de él en todas direcciones. Similarmente a las ondas sobre la superficie de un lago, que forman un círculo que crece en torno al punto donde cayó la piedra, tales ondas de radio forman una esfera creciente en torno al satélite. Esta esfera crece a la velocidad a la que las ondas de radio se alejan del satélite, es decir a la velocidad de la luz. Hay una nueva esfera de ondas de radio alejándose de cada satélite del sistema GPS, en cada fracción de segundo.

Los dispositivos terrestres reciben las ondas de radio emitidas por un satélite. La información transmitida por esa señal contiene la posición del satélite emisor, y la hora precisa en la que fue emitida la señal. Con esos datos, y sabiendo además la hora en la que recibimos la señal, podemos saber a qué distancia estamos del satélite. En efecto: conocemos la hora de emisión y la de recepción, y sabemos que la señal de movió a la velocidad de la luz. Voila!

Notemos que en el momento de recibir la señal, el dispositivo está justo en el lugar donde está pasando la esfera de radio que se aleja del satélite. Al igual que dos círculos diferentes se intersectan en sólo dos puntos, lo mismo es verdad para tres esferas distintas. O sea que en principio recibiendo la señal de tres de los satélites, y calculando a qué distancia estamos de cada uno de ellos, podemos saber exactamente nuestra posición.

(Fuente)

Hay una sutileza aquí, y es que para usar una esfera que se expande a la velocidad de la luz, tendríamos que ser capaces de medir la hora con muy buena precisión. De hecho con mucha más precisión que la sería posible con el reloj de nuestros celulares. Para resolver esto se usa un cuarto satélite: así como tres esferas se intersectan en sólo dos puntos, cuatro esferas que se expanden se intersectan en un punto determinado solamente en un instante determinado. Con esto, no necesitamos confiar en nuestros relojes, y podemos usar los mucho más precisos relojes atómicos que están a bordo de cada satélite.

Por supuesto, para que todo esto funcione, necesitamos asegurarnos de conocer con precisión la posición de los satélites en cada momento. Esto es posible gracias a la mecánica orbital, una teoría física compleja desarrollada por el ñoqui de Isaac Newton, mantenido por el laburo de los pagadores de impuestos británicos del siglo XVII .

Isaac Newton (Fuente)

También tenemos que ser capaces de emitir y recibir ondas de radio. Por suerte los contribuyentes europeos mantuvieron a los parásitos de Michael Faraday, Alessandro Volta, Luigi Galvani, André-Marie Ampere, Heinrich Rudolf Hertz, James Clerk Maxwell y varios otros quienes, sin producir una patente en toda su inútil vida, desarrollaron el electromagnetismo durante los siglos XVIII y XIX.

Michael Faraday (Fuente)

Otro detalle importante es saber operar relojes atómicos. Aquí entra la mecánica cuántica, desarrollada entre otros por Niels Bohr, lejendario parásito de un estado pequeño y pobre como Dinamarca, el cual en la primera mitad del siglo XX no podía permitirse tirar la guita en esas boludeces.

Niels Bohr (Fuente)

Claro, además hay que mantener los relojes atómicos sincronizados entre sí. Si no fuera por el mantenido improductivo de Albert Einstein, que entre 1905 y 1915 de fumó la guita que el estado les robó a los tenderos alemanes, estudiando pajereadas sin ninguna aplicación práctica como la relatividad general, no sabríamos como hacer los cálculos necesarios.

Albert Einstein (Fuente)

Es decir que el GPS, una de las maravillas tecnológicas de las últimas décadas, que genera millones de dólares en beneficios en infinidad de áreas diferentes… no existiría sin la contribución de esos ñoquis mantenidos parásitos que no patentaron una mierda durante tres siglos y se dedicaron a hacerse la paja con guita de otro investigando boludeces sin ninguna aplicación práctica.

Como consejo, la próxima vez que opines sobre ciencia, una buena forma de ubicarte es usar un GPS. Así tal vez evitás quedar como un burro soberbio e ignorante.

Espías en la selección de Camerún

Fuente

Hagamos un experimento sociofutbolístico.

Supongamos que, en su ambición de conquistar el mundo, la dictadora del malvado partido único del colectivismo comunista de Corea del Norte infiltra la selección de la democrática, floreciente y capitalista República de Camerún. Mediante inteligentes maniobras de inteligencia, logran subrepticiamente y sin que nadie lo note acomodar a once espías coreanos como titulares en la selección africana.

Fuente

Sospechando algo, el DT de Camerún decide mezclar a los once suplentes, todos africanos, con los titulares, para luego seleccionar al azar la nueva formación del equipo ¿Cuantos agentes coreanos quedaron ahora en la cancha? Un cálculo sencillo nos dice que, en promedio, hay unos cinco o seis asiáticos entre los nuevos once titulares.

Aún preocupado por los posibles infiltrados, el DT decide repetir el procedimiento. Agrega once suplentes africanos, los mezcla con los titulares, y selecciona al azar a los nuevos once jugadores que jugarán el partido. En esta segunda selección quedarán en promedio sólo uno o dos agentes comunistas entre los miembros de la escuadra verde.

Fuente

Habiéndose formado en las inferiores de un equipo del Conurbano, el DT de Camerun sabe ser suspicaz. Así que repite el procedimiento varias veces más. ¿Cuántos coreanos quedan ahora? Probablemente ninguno ¿verdad? Casi con seguridad tenemos una selección completamente africana, sin un solo villano comunista infiltrado.

El único efecto que el intento de copamiento maoista podría tener en esta nueva selección de Camerún es, tal vez, haberle dejado alguna herencia. Algo de su juego, alguna puteada en su idioma, no mucho más. Si los nuevos integrantes africanos fueran incapaces de recordar nada de lo que pasaba mientras la selección estuvo infiltrada por coreanos, entonces es lo mismo que nunca lo hubiera estado.

~

Un medicamento homeopático es como la selección de Camerún: empezó siendo un veneno, pero se lo diluyó repetidamente hasta que no quedo nada de él, tantas veces que ahora es sólo agua. Y el agua no tiene memoria alguna de aquéllo que tuvo disuelto en el pasado. Luego la homeopatía no puede tener otro efecto que el que pueda tener el agua. Esto es simple sentido común. Pero si no alcanzara, hay además muchos experimentos de tipo doble ciegos que muestran que los medicamentos homeopaticos no tienen efectos sobre la salud.

Fuente

Tener una mente abierta es, antes que nada, usarla. No apelar a mecanismos ocultos e inescrutables o a conocimientos y erudiciones sacerdotales. Eso es pensamiento mágico.