Gulliver y la longitud

(PD)

Mientras preparaba una clase, donde pensaba hablar de giróscopos y barcos, recordé un pasaje de Los viajes de Gulliver, la célebre sátira política de Jonathan Swift, cuya mordacidad hoy se disimula haciéndola pasar por libro para niños.

Gulliver viaja a Luggnagg. una isla lejana donde a veces, en algunas familias, nace un niño con una marca que indica que será un struldbrug, es decir un inmortal. Cuando los lugareños le cuentan esto, Gulliver se maravilla, y fantasea con lo que haría si le hubiera tocado la suerte de ser un struldbrug. El detalle, que sólo le comentan luego de dejarlo desvariar durante varias páginas, es que los inmortales jamás dejan de envejecer. Con los años, los achaques de la vejez se vuelven cada vez mayores hasta ser omnipresentes: el inmortal no puede moverse, no escucha, no ve, ni siquiera puede recordar una palabra oída o leída al pasar a la siguiente.

En su fantasía, Gulliver sueña con los logros humanos que le tocaría presenciar

Añádanse a esto los placeres de ver las varias revoluciones de estados e imperios, los cambios del mundo inferior y superior, antiguas ciudades en ruinas y pueblos obscuros convertirse en sedes de reyes; famosos ríos reducidos a someros arroyos; el océano dejar unas playas en seco e invadir otras; el descubrimiento de muchos países todavía desconocidos; infestar la barbarie las más refinadas naciones y civilizarse las más bárbaras. Vería yo entonces el descubrimiento de la longitud, del movimiento perpetuo y de la medicina universal, y muchos más grandes inventos, llegados a la más acabada perfección.

Recordé el pasaje por la frase en negrita, en la que Gulliver fantasea con asistir al descubrimiento de la longitud, porque resulta que esa es una historia de lo más interesante.

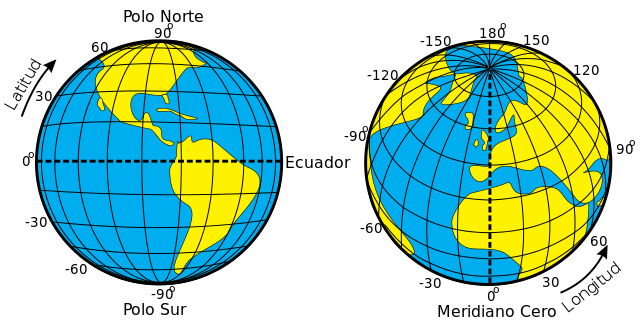
Se refiere a la longitud geográfica, la cual junto con la latitud identifica completamente cualquier punto en la superficie de la Tierra. Los viajes de Gulliver se publicó en 1726, cuando la determinación de la longitud geográfica era uno de los problemas científicos de frontera.

 

(CC0)

La latitud se puede determinar de un modo relativamente sencillo. En el ecuador el sol brilla al mediodía exactamente en el cenit. Al movernos hacia el norte o hacia el sur, lo hace un poco más bajo cuanto más nos alejemos, y cuanto más próximo se encuentre el día más corto del año o solsticio de invierno. Entonces, sabiendo la fecha, y midiendo con un sextante la altura del sol sobre el horizonte al mediodía, se puede obtener la latitud con un simple calculo. Ese método ya se conocía bien en la época de Gulliver.

 

Sextante (PD)

La longitud en cambio, fue un problema abierto durante siglos. La expansión imperial europea requería cruzar los océanos en dirección este-oeste. Al ser incapaces de determinar la longitud, los navegantes no podían estimar cuántos días faltaban para llegar a puerto. Esto hacía imposible prever la necesidad de provisiones, localizar islas donde obtenerlas, y mantenerse lejos de costas peligrosas. Y eso costaba millones, en naufragios y buques perdidos, a los ricos comerciantes venecianos, holandeses, españoles, portugueses y británicos.

Sin embargo ningún emprendedor privado se ocupó de este problema, por considerarlo una apuesta poco segura y potencialmente muy cara. Tuvo que ser un Estado nacional quien se preocupara por dotar a su país de la ventaja estratégica que le daría ese descubrimiento. La primera recompensa para quien descubriera cómo medir la longitud fue puesta por la corona española a fines del siglo XVI. Siendo como eran reyes católicos, se ocuparon de la longitud y no de la bikini [1]. Holanda puso un premio similar en el siglo XVII, e Inglaterra en el siglo XVIII.

 

(CC BY SA 4) by A.Cano.2

La medida de la longitud empieza con la observación de que el sol sale antes cuanto más al este estemos. Eso implica que, en un momento dado, en cualquier punto al este de nosotros será más tarde que en nuestra posición, tanto más tarde cuanto más hacia el este. Entonces, para medir la longitud deberíamos conocer la hora local y la hora de un punto de referencia, por ejemplo el meridiano de Greenwich, o el de París, o el de Chascomús. Sabiendo la diferencia entre esas horas, se puede calcular la longitud.

Conocer la hora local es fácil, basta observar la altura del sol. Pero para conocer la hora de Greenwich se necesita un reloj sincronizado con ella. En esas épocas era imposible mantener un reloj sincronizado en un barco que se balanceaba todo el tiempo ¡los relojes eran de péndulo!

En el siglo XVII Galileo Galilei propuso usar su descubrimiento, los satélites de Júpiter, a modo de un reloj universal en el cielo, para determinar la longitud. El problema es que es muy difícil mantener un telescopio apuntando a Júpiter con la precisión necesaria en un barco que se balancea. Más tarde Edmund Halley propuso usar la Luna de un modo similar: la distancia entre la luna y alguna estrella lejana cambia muy lentamente y sirve como un reloj celeste, con la ventaja es que es mucho más fácil de observar que los satélites galileanos. Durante el siglo XVIII el método lunar se pudo perfeccionar gracias a Isaac Newton, el mencionado Edmund Halley, Leonard Euler y muchos otros, ehh, ñoquis [2] mantenidos con tus impuestos...

(CC BY SA 4 by Michael Daly)

Recién a mitad del siglo XIX fue posible construir relojes lo bastante precisos que funcionaran bien a bordo de un barco. Estos cronómetros funcionaban a cuerda, usando la teoría de la elasticidad desarrollada por otro inútil parásito del Estado [3], Robert Hooke.

El uso del cronómetro fue la marca de la superioridad naval inglesa por sobre las potencias continentales, que usaban el método lunar. Así, Inglaterra se hizo con el dominio del mar, hasta entonces en manos de españoles y portugueses. Un tonto el rey siglo anterior, haber tirado el dinero en esas estupideces en vez de haber invertido en cerveza artesanal [4]...

Mientras tanto por la misma época un tal Heinrich Hertz descubría las ondas de radio. Él mismo decía en ese momento que no servían para nada. Lo hacía extrapolando ideas de Michael Faraday y de James Clerk Maxwell, otros inútiles que investigaban tonterías que no le interesaban mercado [5]. Hacia principios del siglo XX, las costas continentales tenían grandes antenas que emitían continuamente un código conteniendo la hora del punto de referencia, para que al recibirlo los barcos pudieran calcular la longitud. Una de las primeras de tales antenas se instaló en la torre Eiffel.

 

(CC BY-SA 3 by Nitot)

Los métodos para medir la longitud siguieron avanzando durante el siglo XX. Se utilizaron las comunicaciones de onda corta, los cronómetros electrónicos de cuarzo, los satélites de comunicaciones, entre otros. Hoy usamos el Global Positioning System o GPS, que es uno de los logros tecnológicos más formidables del siglo XXI, y que requiere utilizar cálculos de Relatividad General, la teoría sobre cosas inútiles elaborada por el cómodo empleado público que no se ocupaba de resultados prácticos Albert Einstein [6].

Esta es la historia del descubrimiento con el que fantaseaba Gulliver cuando le hablaron de inmortalidad sin leerle la letra chica. Una historia hermosa de ciencia pura y aplicada, en la cual se ve claramente el rol crucial de los estados y el resultado a largo plazo de la inversión pública en desarrollo científico básico. Creo que Gulliver hubiera estado fascinado.

Aclaraciones para los no argentinos:

[1] Referencia al lobbysta pseudolibertario argentino Nicolás Milei, quien se burló en televisión de los científicos diciendo que investigan la patita de la mosca, en lugar de ocuparse de las necesidades reales del mercado como según él habría hecho el inventor de la bikini.

[2] Un ñoqui es alguien que cobra sin trabajar, una expresión que fue aplicada despectivamente a los científicos argentinos por los operadores políticos en las redes del presidente Macri, con el ibjeto de justificar el desguace del mejor sistema científico de Latinoamérica.

[3] Otra expresión usada por los trolls del gobierno argentino contra nuestros científicos.

[4] La derecha argentina legitima su política de ajuste con el discurso del emprendedor, que se queda sin trabajo y en lugar de quejarse se pone a fabricar cerveza artesanal.

[5] Otra referencia a la versión siniestra propalada por el poder argentino de que la ciencia debe ser útil, entendiéndose por ello privada y orientada exclusivamente a ganar dinero inmediato

[6] Más referencias al contexto político: se trata a los científicos de calidad argentinos como meros empleados públicos que viven cómodamente con el esfuerzo de los contribuyentes.

Mis posts se publican en

• Cave Canem (ciencia, opinión)
• Literatops (literatura, citas literarias)
• Diaspora*
• Mastodon
• SteemIt
• Reddit
• Facebook
• Telegram
• Tumblr

También me pueden contactar en

• CuriousCat
• e-mail

Pattern recognition

Jung y el I-Ching

Me escribe un amigo, brillante filósofo amateur sobre temas varios, contándome su última obsesión: la inexplicable certeza del I-Ching.

 

(PD)

Me cuenta que, en su incansable exploración de fuentes de estímulo intelectual, cayó en el oráculo chino casi de casualidad, lo probó... ¡y quedó sorprendido por la certeza de las respuestas que surgían del libro! Parecían hablar de él, de su situación personal, de su vida.

Intrigado, comenzó a investigar y cayó en un escrito de Carl Gustav Jung, quien fuera junto con Sigmund Freud el cofundador del psicoanálisis. ¡Un prólogo al I-Ching! En ese texto, Jung relaciona al I-Ching con el azar, y a éste último con un supuesto funcionamiento íntimo del universo, inseparable de la psique.

El azar es la ausencia de causas y, dado que las causas de cualquier fenómeno se establecen dentro del modelo con que lo explicamos, el azar es simple desconocimiento, la ausencia de un modelo. Jung elabora una teoría que postula una supuesta relación acausal de la mente con los hechos observados. Llama a su teoría Sincronicidad (sólo para que varias décadas después The Police lo usara como título de su mejor álbum).

Por supuesto que Jung está hablando pavadas (y si alguien esperaba que yo dijera otra cosa, es que no me leen). Pero la razón es muy sutil.

Pionero de la impostación intelectual característica del psicoanálisis, Jung asegura que su teoría se fundamenta en nueva física. Supogo que se refiere a la entonces reciente mecánica cuántica, y su trágico error epistémico-político, la interpretación de Copenhagen. No voy a discutir aquí tal interpretación, solo diré que la mente no interviene en el colapso de la función de onda, eso es un error de la mala divulgación, demasiado popularizado.

Jung decía que su idea de conexión acausal funcionaba dando al I-Ching la posibilidad de ser tan certero en la predicción de los hechos. Leyéndolo, se hace evidente que con el I-Ching usó métodos muy psicoanalíticos: leía los hexagramas, y luego los interpretaba siguiendo el modo de "atención flotante" esto-me-sugiere-aquello tan caro a los freudianos.

Le transmití a mi amigo que a mí también me ha sorprendido el I-Ching. Invito a cualquiera a hacer la prueba, es realmente notable. Uno tira las monedas y luego lee el hexagrama, y parece que sin duda, el libro está hablando de su vida. A veces con una certeza increíble.

Ahora bien ¿cómo se explica? Antes de entrar en eso, déjenme referirme a otro fenómeno similar, y también sorprendente.

Dunne y los sueños

En el libro Un experimento con el tiempo (cuyo título, decía Borges, es uno de los mejores exponentes de tal género literario) el americano John William Dunne habla de sus sueños precognitivos.

Dunne era un ingeniero pionero de la aviación, un hombre pragmático con formación científica. Por lo tanto, cuando empezó a tener sueños predictivos buscó una confirmación experimental y una explicación racional. Montó un experimento para ver si sus sueños eran realmente predictivos: los escribía al despertar, antes de olvidarlos, y días después releía lo escrito buscando similitudes con los acontecimientos recientes de su vida.

(CC BY-SA 3.0, by TSRL)

Dunne notó que en su experimento aparecían más coincidencias, de lo que soñaba con lo que le pasaba después, de las que se podrían esperar a priori. Como Jung, creyó que estaba observando una propiedad del universo físico. Él lo interpretó como algo relacionado con el tiempo, en lugar de con el azar.

La teoría del Universo serial que elaboró Dunne para explicar sus observaciones era mucho más precisa (menos chanta, vamos) que la que Jung aplicó al I-Ching. Pero no menos equivocada. Ambos cayeron en la misma trampa: tanto Jung como Dunne eran personas inteligentes, y las personas inteligentes suelen acercarse a la verdad, aunque no lleguen a verla.

Apofenia y pareidolia

Jung intuyó que el I-Ching y el psicoanálisis estaban basados en el mismo fenómeno. Y algo similar pensó Dunne sobre sus sueños precognitivos. Y en eso ambos tenían razón: el fenómeno responsable de las predicciones asombrosas, tanto las del I-Ching cuanto la de los sueños, es el mismo en el que se basa el psicoanálisis. Su error fue creer que se trataba de un fenómeno físico, no lo es. Es un fenómeno psicológico conocido como Apofenia o, cuando nos limitamos a las impresiones sensoriales, como Pareidolia

• Apofenia: consiste en la tendencia de la mente humana a ver estructura en el simple azar, a imaginar en datos aleatorios la presencia de patrones, orden y significado.
• Pareidolia: es la tendencia a identificar formas y contenido en imágenes o sonidos que no contienen información. Puede entenderse como el fenómeno de apofenia aplicado a las impresiones sensoriales.

La pareidolia es lo que nos hace ver caras humanas en una foto de Marte, o escuchar susurros en la estática radial.

 

(PD)

La apofenia es la que nos hace ver estructuras causales, causas y consecuencias, en eventos no-relacionados.

 

(CC BY 2, by Frank Kovalchek)

El I-Ching, la atención flotante del psicoanálisis de Jung, y el registro de sus sueños que hacía Dunne, son disparadores de apofenia: un hexagrama cualquiera del I-Ching, o un sueño escrito al despertar, contienen frases y referencias sin relación inmediata con la realidad. Cuando la mente los lee buscando esa relación, la apofenia se activa e inmediatamente la encontramos. Como al mirar una imagen de Marte buscando una cara.

Cuando sucede una casualidad cualquiera y la encontramos increíble, de nuevo esta funcionando en nuestra mente la apofenia. En efecto, decimos que es imposible tanta casualidad porque queremos ver una causa, una estructura, donde realmente no la hay.

Muchas condiciones psiquiátricas se deben a un desenfreno de la apofenia o de su versión sensorial, la pareidolia. Un cerebro normal crea interpretaciones de la realidad a partir de los datos sensoriales y de la memoria, y luego el lóbulo frontal hace las veces de "crítico" de tales interpretaciones. Cuando tal crítica falla, se exacerban la pareidolia y aparecen las alucinaciones, y la apofenia y aparece el delirio. El ruido ambiente se transforma en voces, las sombras en demonios, muertos o santos, y el trato normal en persecución.

No sólo los oráculos (como el I-Ching, los sueños, o los psicoanalistas) explotan la apofenia. Muchos otros fenómenos culturales también. La astrología, la pseudociencia, las conspiraciones y la religión tienen mucho de apofenia: imaginar estructura donde no hay estructura, orden donde no hay orden, causas donde no hay causas.

La ciencia misma ha caído varias veces en la apofenia. Precisamente una de las virtudes del método científico es que nos permite librarnos de ella. Tal vez incluso deberíamos definirlo como aquéllas reglas que nos permitan identificar patrones sin caer en la apofenia.

Por otro lado, no todo son desventajas: tanto la apofenia como su versión sensorial la pareidolia, son elementos cruciales en el proceso creativo. Ver imágenes que no están, escuchar sonidos mudos, identificar patrones inexistentes, son el primer paso de la creación, tanto en el contexto artístico como en el científico.

El tigre que no estaba ahí

La apofenia es una ilusión psicológica, y parece a primera vista una debilidad de nuestra mente. Sin embargo, tiene una razón evolutiva, darwiniana, para existir:

• Si en una oscilación de las hierbas imagináramos un tigre que no está ahí y saliéramos corriendo, no pagaríamos nada más caro que un ligero consumo de energía.
• Si en cambio no llegáramos a vislumbrar, o descartáramos como una falsa alarma, al tigre que realmente está allí, nos transformaríamos en su cena.

(PD)

Es decir, el falso positivo, el ver una estructura donde no la hay, no hace daño. El falso negativo en cambio, puede matar. Por lo tanto, la evolución favorece las mentes que generan falsos positivos. Por eso la apofenia y la pareidolia son tan comunes en la mente humana.

En ese sentido, la apofenia no es mala, ni es una falla del pensamiento. Es una parte normal del proceso cognitivo. Lo importante es conocerla y mantenerla acotada donde pueda sernos útil, sin suprimirla completamente:

• Si viviéramos demasiado atentos a la apofenia, perderíamos imaginación, dejando de crear de la nada patrones erróneos hasta vislumbrar el correcto.
• Si en cambio no estuviéramos atentos a la apofenia, caeríamos en la alucinación y el delirio, o más simplemente en el pensamiento mágico y el autoengaño.

Por eso, con lo riesgoso que pueda resultar, la actitud correcta es caminar siempre en el filo de la navaja. Dejar rodar la apofenia, crear libremente interpretaciones de lo que nos ofrece la realidad, pero revisarlas críticamente con frecuencia.

 

(CC BY 4.0, by Michal Maňas)

Una catástrofe afortunada

Para ayudar a mi nene en un trabajo para la escuela, estuve leyendo sobre la formación de la Luna. Fascinante.

 

(PD)

Parece ser que la Luna se formó hace 4500 millones de años, poco después de formado el sistema solar, por una colisión gigantesca: la Tierra chocó con un objeto del tamaño de Marte, es decir aproximadamente la mitad del radio terrestre y el 10% de su masa.

A ese planeta temprano se lo denomina Theia, que en la mitología griega era la madre de la diosa de la luna, Selene. Theia orbitaba en torno al Sol en la misma órbita que la Tierra, pero separada un cierto ángulo, cerca de uno de los puntos de Lagrange conocidos como L4 o L5.

(CC BY-SA 3.0, by Besnier.m)

Los puntos de Lagrange son puntos estables del sistema Tierra-Sol, donde se acumula la basura que no cae en ninguno de esos cuerpos celestes. Theia se formó en uno de esos puntos, a partir de las rocas y el polvo que no cayeron hacia la Tierra durante su génesis, y sobrevivió allí.

Eventualmente, un pasaje cerca de Venus desestabilizó a Theia, que se acercó a la Tierra y la impactó catastróficamente. El impacto arrancó un pedazo de la Tierra y calentó horriblemente el planeta, vaporizando y/o fundiendo buena parte de la corteza. El pedazo arrancado orbitó muy cerca de la tierra y empezó a acumular parte del material desprendido, transformándose en la Luna.

 

(PD)

Lo interesante es todo lo que se puede saber de esta colisión ocurrida hace 4500 millones de años, usando evidencia geológica y selenológica.

• El eje de rotación de la Tierra y el de la órbita lunar son muy similares, eso es prueba del origen común de ambos cuerpos en un impacto.
• Sabemos el ángulo del impacto, porque s deduce deexplica la inclinación de estos ejes respecto de la órbita terrestre, que incidentalmente es la causa de las estaciones.
• Sabemos el radio aproximado de Theia, porque así se explica la cantidad de rotación (momento angular) del sistema Tierra-Luna.
• Sabemos que la colisión no vaporizó el completamente nuestro planeta, porque los elementos pesados (hierro, níquel) quedaron en la Tierra, habiendo muy poca cantidad de elloso en la Luna.
• Para que la colisión no haya vaporizado completamente el planeta, la velocidad del impacto tiene que haber sido relativamente baja, menos de 5km/s. Eso implica que Theia tenía una órbita muy similar a la de la Tierra. Tal órbita sólo es posible si estaba cerca de un punto de Lagrange.
• Sin embargo, sabemos también que el impacto vaporizó una parte de la corteza terrestre, porque en la Luna casi no hay elementos volátiles.
• Un detalle interesantísimo es que parte del material vaporizado (principalmente silicio) formó una atmósfera caliente común a ambos cuerpos. Las cortezas terrestre y lunar capturaron de esa antigua atmósfera, resultando en una composición similar (relaciones isotópicas).

Inicialmente la Luna estaba mucho más cerca de la Tierra. La cara cercana sentía la gravedad terrestre con mucha más fuerza que la lejana. Esas fuerzas de marea provocaron que la cara más pesada de la Luna quedara trabada mirando siempre hacia la Tierra.

A medida que la Luna se enfriaba, las mencionadas fuerzas de marea provocaban fracturas en su superficie, haciendo aflorar la lava. Estas grietas eran más frecuentes en la cara cercana, en la que sque sentía más fuertemente la atracción de la Tierra. Por eso esa cara está cubierta de maria: las manchas grises de la Luna, que llamamos "mares", son en realidad afloramientos de lava, ya fría, provocados por ese proceso.

 

(CC BY-SA 3.0, by Peter Freiman)

Las fuerzas de marea deforman ambos cuerpos, los amasan. En ese proceso, disipan energía, transformándola en calor. Eso frena a la Luna. Y a medida que se frena, la Luna se aleja de la Tierra (porque se cumple la tercera ley de Kepler). Eventualmente en el futuro, escapará. Selene, la hija de Theia, ganará de este modo la libertad que nunca tuvo desde su trágico nacimiento.

 

(PD)

Como especie, somos afortunados de tener a la Luna tan cerca nuestro. La Luna fue causa de muchos hechos cruciales de nuestra existencia

• La gravedad de la Luna provoca las mareas. En el pasado lejano, las mareas dejaban algas sobre las playas. Estas algas eventualmente evolucionaron para colonizar los continentes, transformándose en las plantas terrestres.  (CC BY-SA 3.0, by mabelcalabuig)
• De manera similar, las mareas dejaban atrópodos en las playas, animalitos similares a camarones y cangrejos. Estos evolucionaron para transformarse en los insectos terrestres.
  (PD)
• Finalmente, en tiempos mas recientes las mareas dejaron peces en las playas. Estos peces desarrollaron patas y la capacidad de respirar aire... y aquí estamos nosotros, el resultado de la evolución de los vertebrados terrestres.
  (CC BY-SA 3.0, by Gianluca Polgar)
• Nuestros antepasados prehistóricos eran serres curiosos. Al mirar al cielo comenzaron a preguntarse que era ese disco brillante que iluminaba la noche, y por qué tenía fases y eclipses. E intentado responder a esa pregunta, inventaron lo que hoy llamamos ciencia.
  (CC BY-SA 3.0, from Wikimedia)
• El avance científico nos llevará, eventualmente, a colonizar el sistema solar. Para hacerlo, casi sin dudas empezaremos por la Luna. Por su cercanía y su baja gravedad, la Luna es ideal como puerto, para recibir y enviar naves, con suministros y colonos, hacia otros planetas.
  (PD)

Así, los seres humanos existimos, evolucionamos, y con suerte sobreviviremos, gracias a la existencia de la Luna.

La apoteótica destrucción de Theia fue una catástrofe afortunada.

---

Post scriptum: disneylandias

Esta es una excelente noticia. Realmente hay disneylandias en la Luna, es decir enormes cavernas subterraneas habitables.

La Luna es un accidente afortunado. Un cuerpo celeste cercano a la Tierra, con abundante luz y gravedad lo bastante alta para poder habitarlo cómodamente, y a la vez lo bastante baja como para poder orbitar sin usar cohetes, con catapultas electromagnéticas. Es un puerto natural. Una Luna poblada sería nuestra base de partida para el resto del sistema solar. Algo muy difícil de hacer directamente desde la Tierra.

Pero es un accidente natural, no una bendición de Dios. Poblarla no es nada fácil, más que nada por su ausencia de campo magnético. Salvo cuando vemos una brújula, el resto del tiempo no pensamos en el campo magnético terrestre. Pero es un elemento fundamental que garantiza que estemos vivos.

El campo magnético desvía el viento solar hacia los polos, causando las auroras boreales, y evitando que esa radiación nos alcance. Sin campo magnético, la radiación del viento solar llegaría al suelo y sería letal. El embate del viento solar es tan fuerte que incluso en Marte, donde es mucho más débil, arrastró al espacio buena parte de la atmósfera. Ignoro si hubiéramos podido evolucionar sin el escudo que el campo magnético nos proporciona.

 

(PD)

La luna no tiene campo magnético. El viento solar llega al suelo. Podríamos tolerarlo durante unos días. Incluso durante una vida. Pero no por generaciones. Por eso los asentamientos humanos en la Luna deberán ser subterráneos (al menos hasta disponer de imanes superconductores gigantescos que puedan generar un campo artificial).

Siempre se sospechó que la Luna tenía cavernas subterráneas del tamaño de ciudades. El autor de ciencia ficción John Varley las llama disneylandias en sus historias de Los ocho mundos (que recomiendo, lean por ejemplo las excelentes novelas El globo de oro o Playa de acero o los cuentos de Blue Champagne). Esta noticia es la confirmación de que en efecto existen, y que no tendremos que excavar la roca para construir refugios. Es excelente.

 

(PD)

Una vez mas, la espectacular muerte de Theia se empeña en ser una catástrofe afortunada.

Tiempos imaginarios

La tinta, la crema, el azúcar, o el calor

En la imagen se ve una gota de tinta en agua. Imaginen como se diluye lentamente, volviéndose más transparente. Ese fenómeno se llama difusión.


(CC BY-SA 4.0, by Zvonimir Lončarić)

La difusión es un proceso físico por el que se trasmite energía y materia de un punto a otro del espacio. No sólo a gota de tinta en el agua obedece al fenómeno e difusión

• Cualquier sustancia (materia) que se pueda disolver en un solvente se difunde en él. La tinta en el agua, el azúcar o la crema en el café, y casi cualquier ejemplo que podamos imaginar.
• El calor (energía) se difunde en los cuerpos. La resistencia de la plancha genera calor que se difunde en el metal, y al tocar la tela de la camisa también se difunde en ella.

La difusión funciona de un modo muy sencillo, es una tendencia a igualar concentraciones. Se describe con una ecuación bastante simple, que voy a intentar escribir acá. No se asusten, es muy fácil, y es lindo entender cómo se usan las ecuaciones para explicar la realidad.

Supongamos que tenemos una región del espacio con una parte que podemos llamar su interior y una superficie que hace las veces de frontera. Podría tratarse de una gota dentro de un vaso lleno de agua. Supongamos que esa región llena de alguna cosa cuya difusión queremos describir. Por ejemplo, la gota podría contener tinta.


(PD)

El contenido abandonará la región a través de su frontera. La tinta sale de la zona inicialmente más oscura a través de la superficie que rodea esa zona. Podemos establecer una ley sencilla para describir este fenómeno:

La cantidad de contenido que se escapará en cada segundo desde el interior, será proporcional a la diferencia entre la concentración interior y la concentración exterior, y también a la superficie de la frontera.

¿Suena complicado? Leelo de nuevo, es muy sencillo: el mundo tiende a la homogeneidad.

• Si dentro de la región la tinta está muy concentrada, y fuera está muy diluida, la cantidad de tinta que atraviesa la superficie por segundo será mucha.
• Si en cambio la concentración dentro es apenas mayor a la concentración fuera, la tinta escapará muy lentamente.
• Y por supuesto, si la concentración fuera es mayor que la concentración dentro, la tinta entrará en la región en lugar de escapar de ella.

Se trata simplemente de la tendencia a emparejarse que tienen las cosas. Una especie de búsqueda de la homogeneidad.

Escribamos una ecuación para describir el fenómeno. La concentración de tinta es el número de moléculas de tinta dividido el número total de moléculas. O sea, es la probabilidad P de que al tomar una molécula al azar, esta sea de tinta y no de agua.

Si N es el número de moléculas dentro de la región, y dN su cambio en un lapso de tiempo dt, la ecuación es

dN = k (Pe - Pi) S dt

siendo Pe la concentración exterior y Pi la interior, S la superficie de la región, y k una constante que caracteriza el proceso en cuestión.

Esta ecuación de difusión es simplemente la expresión matemática de lo que explicamos antes. Si la fórmula no se entiende, no importa mucho, no contiene nueva información más allá de lo que dice el texto.

Esta ecuación controla los procesos físicos de disolución de materia o de energía. Nos dice como se difunde la tinta en el agua, el azúcar o la crema en el café, o el calor en la plancha.

Los electrones, los protones y demás objetos pequeños

Lo interesante es que la ecuación de difusión se parece mucho a la ecuación de Schrœdinger, que describe la mecánica cuántica de los objetos muy pequeños como las partículas subatómicas.


(PD)

La ecuación de Schœdinger para una partícula se puede escribir así

dN = i h (Pe - Pi) S dt

Donde ahora N es una medida de la probabilidad de encontrar la partícula dentro de la región, Pe y Pi la de encontrarla a cada lado de la superficie, i la raiz cuadrada de -1, y h una constante conocida como constante de Planck.

Como vemos, la ecuación es muy parecida... casi parece que si le cambiáramos el nombre a h y la llamáramos k quedaría igual... salvo por esa maldita i metida ahí adelante... Si quisiéramos leer la ecuación para entenderla en palabras que entendimos la ecuación de difusión ¿Qué rol cumpliría esa i?

La salvedad aquí es que en mecánica cuántica N y P no son realmente probabilidades sino amplitudes, es decir números que en principio pueden ser complejos. Luego podemos identificar nuestra constante de difusión con k = i h, y la interpretación en palabras es la misma que antes

La cantidad de contenido (amplitud) que abandonará la región en cada segundo , es proporcional a la diferencia entre la amplitud interior y la amplitud exterior, y a la superficie de la frontera.

No suena mal. El único problema es que, siendo la amplitud un número complejo, perdemos la intuición acerca de cosas que sem hzan de un lado y de otro de la superficie.

Sin embargo, hay otra interpretación posible. Cambiemos el nombre k = h y redefinamos la manera en la que medimos el tiempo transcurrido como dT = i dt. De nuevo la ecuación se lee así:

La cantidad de contenido (amplitud) que abandonará la región en cada segundo imaginario, es proporcional a la diferencia entre la amplitud interior y la amplitud exterior, y a la superficie de la frontera.

Y o si la amplitud es inicialmente nr el, alo ber una i en la ecuación se mantendrá real al transcurrir el tiempo, y con eso recuperamos la intuición de cosas que se homogeneizan que teníamos con la difusión de la tinta.

Todo muy lindo, pero... ¿qué demonios sería un segundo imaginario?. Y aquí entra el pragmatismo de los físicos: n segundo imaginario es una forma conveniente de transformar la ecuación de Schrœdinger en la ecuación de difusión, manteniendo k real.

Con esta reinterpretación de la ecuación de Schœdinger, podemos decir que los electrones, los protones, o as las partículas subatómicas se difunden en el espacio como si fueran tinta, solo que lo hacen cuando el tiempo corre en la dirección imaginaria.

-- Pero pará, el tiempo el tiempo es un número real, mi reloj no marca números imaginarios. Un tiempo imaginario significa que el universo...

-- ¡Callate y calculá!

Sucede a menudo que situaciones físicas muy diferentes entre sí se vuelven similares si imaginamos que el tiempo pueda ser un número imaginario. Si esto es una simple coincidencia matemática o si tiene alguna interpretación más profunda, es algo que nadie sabe.

Pero ¡guau! ¿no?

Mis posts se publican en

• Cave Canem (ciencia, opinión)
• Literatops (literatura, citas literarias)
• Diaspora*
• Mastodon
• SteemIt
• Reddit
• Facebook
• Telegram
• Tumblr

También me pueden contactar en

• CuriousCat
• e-mail

Cuidar a tus hijos... ¿o tener muchos?

En base a una pregunta que me hicieron en CuriousCat, me puse a leer sobre el modelo r/K en ecología. Fascinante.

(CC0)

Para empezar, el sentido de la vida. Lamento arruinarles la Guia del autostopista galáctico y toneladas de libros de filosofía, pero la razón por la que estamos vivos es sencilla: lograr que la información codificada en nuestros genes se propague a la siguiente generación. Somos sólo máquinas copiadoras de genes. Lo demás es autoayuda.

El objetivo último de la existencia de cualquier organismo vivo es maximizar el número de copias de sus genes que lo sobrevivirán una generación más. Para lograrlo, un ingrediente fundamental es, claro, el tener descendientes. Pero otro punto no menor es también que estos lleguen a adultos y tengan, a su vez, descendientes.

(PD)

Se puede escribir una ecuación para entender la dinámica ecológica que surge de esa regla. Si el número de individuos es N y cada uno tiene r descendientes, el número de descendientes será r N. Sencillo ¿no?

Pero ¿cuántos llegarán a adultos?

La proporción del total descendientes que llegarán a adultos será mayor cuanto mayor sea el cuidado K que los padres pongan en ellos. Y será menor cuanta más competencia tengan que enfrentar, o sea, cuanto mayor sea el número de adultos, N. Para incluir esa información en nuestra fórmula, podemos definir la proporción 1 - N/K, que será igual a 1 cuando no haya otros adultos vivos al momento de nacer los descendientes, y a 0 cuando el número de adultos vivos sea tan grande, que todo el cuidado que los padres puedan poner en sus hijos no alcance para hacerlos sobrevivir a la dura competencia.

Con esto, el número de descendientes que llegarán a adultos en cada generación, que se escribe dN/dt, vendrá dado por la ecuación del modelo r/K, que se escribe

dN/dt = r N (1 - N/K)

Lo relevante de esta ecuación es que, al escribir un modelo matemático del problema, aislamos los parámetros fundamentales que lo definen. En este caso r, el número de descendientes, y K, la inversión de esfuerzo paterno en la cría de los hijos.

Es obvio que r y K no son independientes: quien tiene muchos hijos no puede invertir mucho tiempo en cuidarlos. Hay que elegir. Esto nos permite identificar dos estrategias posibles:

• Hay especies que eligen maximizar r olvidándose de K. Son en general animales pequeños, que tienen muchas crías, a las que casi no cuidan y que maduran muy rápido. 
  

      (CC BY-SA 3.0 , by Christian Fisher)

• Otras especies en cambio, maximizan K mientras mantienen un r pequeño. Son en general animales grandes, que tienen pocas crías a las que cuidan mucho, y a las cuales les toma mucho tiempo madurar. 
  
  (CC BY 2.0, by Derek Keats)

Cada especie elige un compromiso entre r, el número de descendientes, y K, la inversión de los padres en cuidarlos. Algunas apuestan más por r, otras más por K. Y en las especies más complejas ese compromiso cambia según las condiciones del entorno. Lo que es también fascinante.

• En entornos ecológicamente estables, el futuro es previsible. Vale la pena invertir esfuerzo en criar pocas crías porque, casi con seguridad, llegarán a adultas. Los entornos ecológicamente estables favorecen la estrategia K.
• En entornos ecológicamente inestables, el futuro es imprevisible. Conviene tener muchas crías e invertir poco esfuerzo en ellas, ya que es probable que la mayoría mueran antes de llegar a adultas. Las catástrofes y la imprevisibilidad favorecen la estrategia r.

Y ahora viene lo más polémico y vuela cabezas del asunto: pensemos en la especie humana. La estrategia de la especie es predominantemente K, pocos hijos que maduran lento con gran inversión parental. Pero ¡cambia según las circunstancias!

• Las clases altas, los habitantes de los países desarrollados, la gente que vive en entornos estables y previsibles, tiene pocos hijos que maduran muy lentamente, en los que invierten mucho esfuerzo. Estrategia K. 
  (PD).
  
  
  Las situaciones de bienestar (riqueza, sociedades y economías estables) favorecen las familias chicas y los adolescentes inmaduros.
• Las clases bajas, los habitantes de los países pobres, la gente que vive en entornos poco previsibles, tiene muchos hijos que maduran muy rápidamente y en los que invierten comparativamente poco. Estrategia r. 
  (PD)
  
  
  Las situaciones de catástrofe (guerras, calamidades, pobreza extrema) favorecen las violaciones y el abandono de niños, y la sexualidad precoz.

Fascinante. No importa que tan complejos nos guste creer que somos, en el fondo obedecemos reglas relativamente sencillas y similares a las de las demás especies.

Por supuesto que el modelo r/K es una idealización, y que las realidades ecológica y humana son mucho más complejas. Pero su función, como la de cualquier modelo, es singularizar los aspectos importantes que controlan la dinámica de un sistema. Y siempre se puede mejorar a posteriori incluyendo más variables y más interacciones entre ellas.

Lo que es impresionante es el poder que tiene un modelo tan sencillo para poner en un solo marco muchas observaciones aisladas. Es la belleza de la matemática aplicada al mundo cercano.